ChatGPTさんと学ぶ幾何ブラウン運動(まるでわからん→ちょとだけわかるの軌跡)
前回の夏(7月)のブログ記事から随分日がたってしまいました。もう秋(11月)ですね。時のたつのは速いものです。
今日は前回までの投資シミュレーション系の記事で使用した幾何ブラウン運動 (GBM)について備忘ログを残しておこうかと思います。ですが、今回の記事は、幾何ブラウン運動についてつまびやらかに解説を行う記事ではないです。筆者(midori)がChatGPTさんに作ってもらった幾何ブラウン運動のプログラムについてなんもわからんからちょいわかったに移ろいだ過程について備忘ログとして残しておくという記事です。読者さまへのお役立ち度は少ないかな(遠い目)。
幾何ブラウン運動で株価シミュレーションデータを作りたい
株価の値っぽい時系列ダミーデータを生成しまして、その時系列のダミーデータを使って未来における投資信託の利益率を計算したかったのです(前回の記事)。「株価の値」っぽい時系列データをどうやって作ったらいいのでしょうか? 株価とは、以下のようになんかじぐざぐしております。どうやってこのジグザグを作ったらいいの? 乱数でもばらまくの?
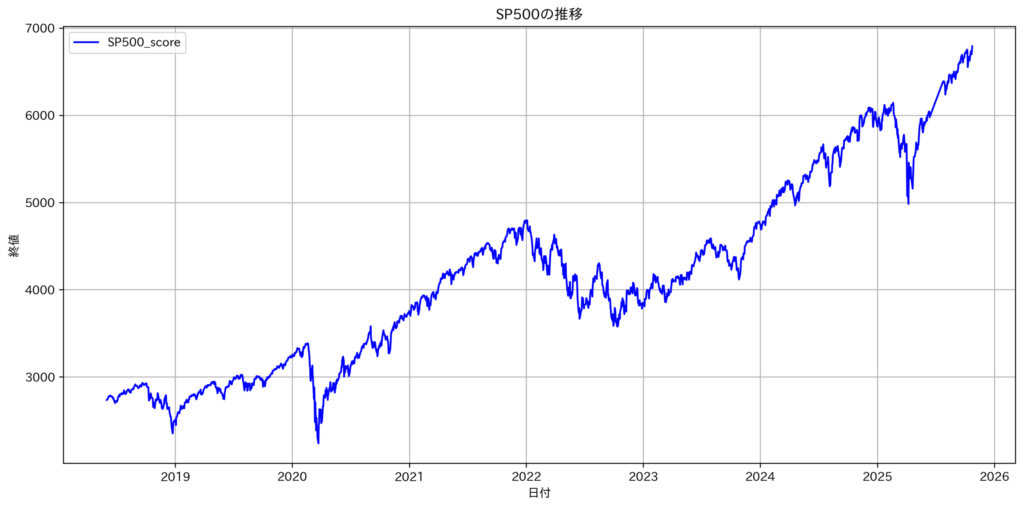
困ったことがあったらなんでもAIに聞いていきましょう。私が「このジグザグ作りたいんだけどどうしたらいいの?」とお願いをChatGPTにしたら、幾何ブラウン運動に基づくpythonコードをおすすめされたわけです。
幾何ブラウン運動とはなにか
そもそも幾何ブラウン運動ってなんだろう? Wikipediaの「幾何ブラウン運動」の記事によりますと、
幾何ブラウン運動 (きかブラウンうんどう、英: geometric Brownian motion; GBM) は、対数変動が平均μ分散σのブラウン運動にしたがう連続時間の確率過程[1]で、金融市場に関するモデルや、金融工学におけるオプション価格のモデルでよく利用されている。幾何ブラウン運動の増分が St に対する比として表されることから幾何(geometric)の名称がつけられている。[2]
とのことです。ううむ? よくわからんな。そもそもブラウン運動とはなんなのか・・・?
ブラウン運動とはなにか?
Wikipediaの「ブラウン運動」の記事によりますと、
物理学におけるブラウン運動(ブラウンうんどう、(英: Brownian motion)は浮遊する微粒子が不規則に運動する現象である。
ブラウン運動は確率過程として数理モデル化できる。具体的にはウィーナー過程がそのままブラウン運動のモデルとみなせる(そのため数学ではウィーナー過程を別名「ブラウン運動」とも呼ぶ[14])。
とのことです。ふむ。なるほど、今度は、確率過程がわからん。
確率過程とは何か?
Wikipediaの「確率過程」の記事によりますと、
確率論において、確率過程(かくりつかてい、英語: stochastic process)は、時間など,条件によって変化する確率変数の数理モデルである。株価や為替の変動、ブラウン運動などの粒子のランダムな運動を数学的に記述する模型(モデル)として利用している。不規則過程(英語: random process)とも言う[1]。
とのことです。わかりません。他の確率過程に関するブログ記事を読んでみましょう。
確率過程とは?-具体例で解説-
https://data-viz-lab.com/establishment-process
確率過程は、正式には以下のように定義されます。
【定義】
各 t ∈ [0, ∞)に対して、確率変数Xt が与えられたとき、その族X = (Xt)t ≥0を確率過程(stochastic process)という
よくわからんない。族て? 他の幾何ブラウン運動のブログを読んでみよう。
【金融工学】日経平均株価に対する幾何ブラウン運動のフィッティング
https://qiita.com/y-yamamoto-snt/items/bd12300e156dddcd0912
こちらのブログを読んでみました。「指数型微分方程式」とか「対数リターン」とか、今の私には理解がおいつかなかったです。金融工学というらしいのですが、強いKOTODAMA(言霊)を感じます。でも、さっぱりわかんない。ランダムを工学しようってことは伝わってきました。
幾何ブラウン運動の理屈はよくわかりませんでした。

ブラウン運動で筆者(midori)はpythonプログラムで何をやったのか
ブラウン運動の理屈はよくわからんですが、では、次に、ChatGPTさんが作ってくれた幾何ブラウン運動で株価シミュレーションデータを作るためのpythonプログラムについてご紹介いたします。その原理についてはいまいわかっていませんが、プログラムは動いて株価のシミュレーションデータは作ることができたので、「動けばええねん」の心持ちで備忘ログを残しておきます。
株価のシミュレーションデータですが、まずは株価時系列データの基本ラインを引くことから始まります。例えば、株価の初期値がいくらで、終わりの値がいくらで、右肩上がりなのか、右肩下りなのか、など大まかな時系列データの形を決めます。
まずは、右肩上がりのトレンド(trend)を作る例を説明します。pythonコードから抜粋して説明します(importなどは省略です)。
import numpy as np
def _generate_trend(self):
"""生成されるトレンドの骨格(ノイズなし)"""
if self.trend_type in ['up', 'down']:
trend = np.linspace(0, 1, self.days)
return_trend = self.start_price * (self.end_price / self.start_price) ** trend
# 省略
trendには以下のような、numpyのlinespace関数を用いて、1から1.0までの値が0 から 1 までを等間隔に分けた配列ができます。0から1へupしていく値の配列です。このような操作を指数補間(exponential interpolation)というのだそうです。線形補間(start→endをまっすぐ結ぶ)ではなく、「比率が一定になるように」滑らかに変化させるためにこの式を使います。0から1までの値をSP500の値のスケールに変換しているのです。
trend = [0.0, 0.111…, 0.222…, …, 1.0]
このtrendを日付と対応づけてグラフ描画してみましょう。できあがった時系列ラインはこちら。
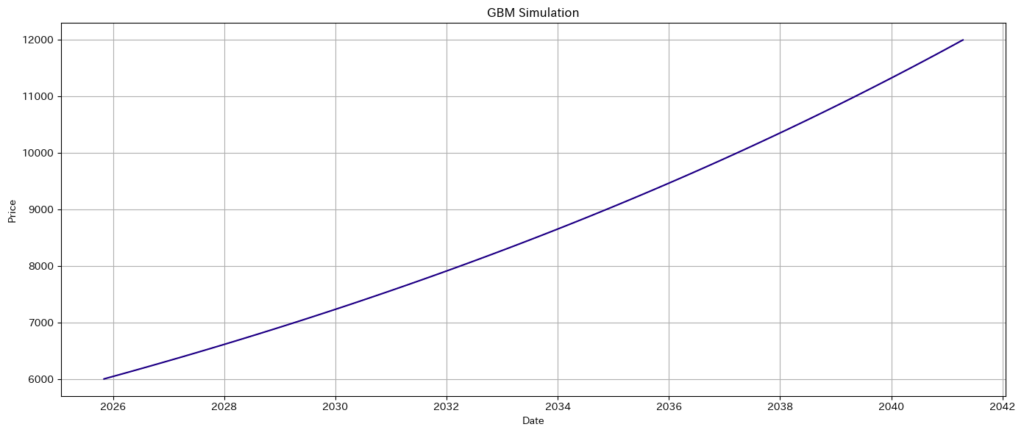
線がまっすぐです。株価らしくないのです。こちらに株価らしいジグザグを付与するにはどうしたらいいのでしょうか? ChatGPTさん曰く、ここでブラウン運動によるノイズを乗っけるといいます。
幾何ブラウン運動の微分方程式を解いて株式データっぽいノイズを作る
ノイズはランダムさを表すデータで、以下のようにして生成します。
def _generate_gbm_noise11(self):
# 乱数を得る
np.random.seed(self.random_seed)
# (対数リターン)
# log の項は株価や指数などの 「1日ごとの変化率を、対数で表したもの」 = 「1日で価格がどれだけ増減したか」( 対数リターン)
# np.log(self.end_price / self.start_price) が全期間の対数リターン、これをself.daysで割って1日あたりの平均成長率 μ(日単位)とする。
mu = np.log(self.end_price / self.start_price) / self.days
# 正規乱数(ホワイトノイズ)
# epsilon は平均0・標準偏差1の正規乱数(ホワイトノイズ)
# 長さ self.days の配列なので、日ごとに違うランダム要素となります。
epsilon = np.random.normal(0, 1, self.days)
# 1年のビジネス日数
dt = 1 / 252
# (幾何ブラウン運動の微分方程式の解)
# sigmaは価格の「揺れの大きさ」=ボラティリティ(volatility) を表す数値です。大きいほど値の変動が大きくなる。
# (mu - 0.5 * self.sigma**2) * dt は平均的な株式成長成分(ドリフト部分)
# self.sigma * epsilon * np.sqrt(dt) はランダムな揺らぎ成分(ボラティリティ部分)
# (微分方程式の解をlogで表した式)
returns = (mu - 0.5 * self.sigma**2) * dt + self.sigma * epsilon * np.sqrt(dt)
return returns
「幾何ブラウン運動の基本式の解」の箇所ですが、そもそも幾何ブラウン運動の基本式は以下のようになります。

幾何ブラウン運動の基本式は微分方程式の形で表されます。微分方程式は変化の仕組みを表すものです。dSt は 微小時間 t での値動き、μStdt は平均的な成長率、σStdWt はランダムなノイズから構成されます。「価格の変化 = 平均成長(トレンド) + ランダムなノイズ(変動)」で表すということです。
この微分方程式を解いて対数をとったものが以下の式になります。
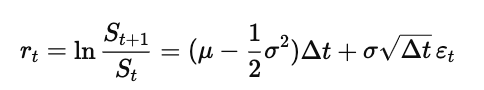
ここば↑のプログラムでの(微分方程式の解をlogで表した式)にあたるのです。(式変換の導出はできてないですが、なんとなくあってそう)
基本のラインにノイズをのせる
右肩あたりの基本ラインにノイズを乗っけるコードは以下となります。
def generate(self):
# 基本線を描きます
base_trend = self._generate_trend()
# 対数リターン
log_returns = self._generate_gbm_noise11()
# 累積リターンを指数化して価格比に変換
noise_factor = np.exp(np.cumsum(log_returns))
# ノイズを乗っけます
prices = base_trend * noise_factor
# 最後の仕上げに、dataframeでビジネスデーの列データを作りまして、まっすぐの株価データとくっつけます。
today_str = date.today().strftime('%Y-%m-%d')
dates = pd.bdate_range(start=today_str, periods=self.days)
self.df = pd.DataFrame({'Date': dates, 'Price': prices})
return self.df
できあがったpandasのdataframe(self.df)をmatplotlibでグラフ表示しますと以下のようになります。
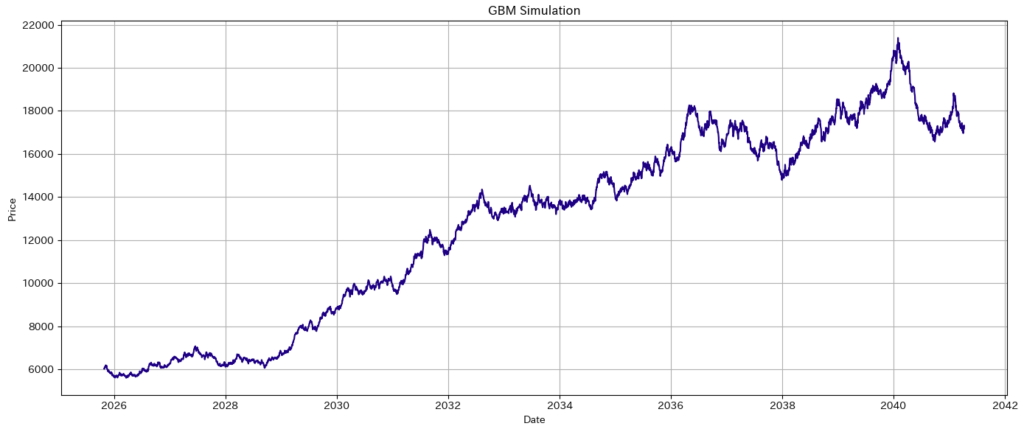
右肩あがりのトレンドでノイズがのったラインがひけました! 株価のシミュレーションデータとして使えそうです!
ChatGPTさんと学ぶ「幾何ブラウン運動」まとめ
確率過程とか、金融工学とか、数学が難しくて理解できなかったですが、AIでpythonのコードを生成することで、実際に株価のダミーデータを作ることができました。やはり現物のデータがあると理解につながるような気がします(気がするだけかも)。また、ChatGPTさんの幾何ブラウン運動の解説を読むと、幾何ブラウン運動の考え方もなんとなくわかったような気がします(本当はちゃんとした教科書で裏取りをしたいものです。でもラインが引けてるからおおはずしはしてないはず)。今後は、理論的な背景について、もっと深く勉強していきたいです。


